The Wilson effect

When researchers estimate heritability from twin studies either longitudinally or cross-sectionally, one result almost always replicates: as individuals grow older, heritability estimates of behavior tend to increase, for some phentoypes like IQ by extreme amounts. This is the Wilson effect. The usual corollary to this finding is that while heritability increases, the effect of the shared environment(but not of the unshared environment) tends to evaporate.

In this article I consider different explanations for this finding: Measurement error, Phenotype→Environment models, and AxC(gene by shared environment) interactions.

Some basics first:

Twin studies can be used to estimate (usually) three variance components:
A(variance explained by additive genetic variance)
C(variance explained by the environment that all twins share)
E(variance due to everything else, like nonshared environmental effects, measurement error)
Classical twin studies assume a few things:
DZ twins have a genetic correlation of 0.5, MZ twins have a genetic correlation of 1.0, there are no interactions between the three estimated parameters, DZ and MZ twins share their environments to the same extent, and that the three variance components are not correlated with each other. Given these assumptions, we can estimate the ACE model. Nowadays the most popular method is to fit a Structural Equation Model. This model basically iterates over possible values for all the latent factors(A,C,E), and tries to minimize the objective function, which is defined by the difference between the observed and predicted covariance matrices. The predicted covariances can be calculated by hand or by following path tracing rules.
In the example path diagram below, P1 stands for the phenotype of the first born twin, and P2 for the second born twin. Of course the reverse would result in the same estimates.

Following basic covariance algebra, the implied variance-covariance matrix of this model is :

Using the matrix, we can derive:

Therefore, additive genetic effects can be estimated by taking the difference between the MZ and DZ correlation and doubling it. Slight caveat: If nonandditive genetic effects are present, then this formula captures most of that too. Since nonandditive genetic effects seem to be weak, I will not consider them in this article.

Now that we know the basics, we can try to solve the mystery.

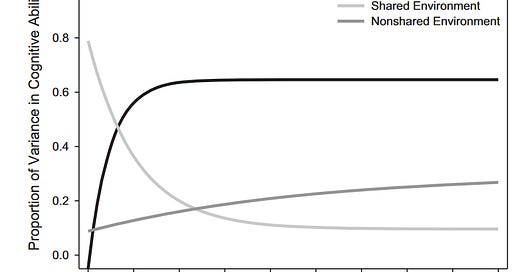
1: Let’s start with measurement error. It’s a fairly well known fact that IQ is quite stable in adults, however childrens’ IQ scores are much less stable. Since measurement error goes into the nonshared environment(E) component, if this is the explanation, then we should see that the increase in heritability is coupled with a decrease in the nonshared environment. This is not the case(¹):

2: Phenotype→Enironment models.
There are many theoretical and statistical P→E models(Scarr &McCartney 1983, Dickens&Flynn 2001, De Kort et al 2012 , Beam et al 2015 and probably many more)
The common theme of these models is that people with certain phenotypes are more likely to self-select or get pushed into certain environments. A bright student might seek out extra learning opportunities, an athletic student is more likely to be scouted by coaches, thereby compounding their “innate” or acquired advantages. P→E models have been used to argue that potent environmental effects can be present, even if the heritabilities are extremely large(Dickens&Flynn 2001, see also De Kort et al 2014)

Does the data support such theories? In short: yes.
De Kort et al 2014 sought to answer whether P→E models can explain the Flynn effect. They fit a standard ACE Simplex(a standard ACE model with multiple timepoints) model, and a P→E model. They found that models both fit the observed twin data well. The P→E model had slightly better fit, however direct comparison was not possible, since the models are not nested. The P→E model estimated correlations between 0.32-0.66 between A and E, with the correlation increasing over time.

Beam et al 2015 used a slightly different, multilevel(between and within-family) genetic simplex model, and estimated the within-family P→E effects(red lines):

The majority of the effects were positive, providing tentative evidence that P→E mechanisms may be present within family too:

Beam&Turkheimer 2013 simulated data assuming within-family P→E effects, and found that they result in stable MZ , but declining DZ twin correlations over time.

This phenomenon is exactly what we see in real twin data too for weight, and intelligence, but not height (Beam&Turkheimer 2017):

Since we know that we can calculate heritability as 2(pmz-pdz), a stable MZ correlation with a falling DZ correlation increases heritability estimates.

3: The final contender for the explanation of the Wilson effect is that of gene-environment interaction, specifically AxC interaction.

Purcell 2002 reminds us that unmodelled AxC gets absorbed by the A component in ACE models. AxC is notoriously hard to detect, with even the best twin-based methods having very low power(Molenaar et al 2012).
If AxC exists, then it’s a reasonable hypothesis that older individuals have more variance due to it, because they have experienced more AxC during their life(Fischbein 1978). An easy way to understand this is to first consider MZ twins. Since they are genetically identical, if they share an environmental exposure, then their reaction to that cannot differ due to their genes, therefore their correlation remains stable. On the other hand, since DZ twins are not genetically identical, if they share an environmental exposure, it is possible that their reaction is different due to their genes, therefore their phenotypic correlation falls over time.

Since there are zero well powered twin methods to detect AxC,and genomic studies such as Andersen et al 2021 used adult measures of SES(a potential environmental variable that is likely to interact with additive genetics), we will have to wait for emerging studies to evaluate this hypothesis.

There are reasons to be hopeful though. Robinson et al 2017 and Moore et al 2018 both found evidence that GxE is present for BMI using genomic methods, and Molenaar et al 2015 found evidence that both AxC and AxE is present for behavioral and emotional problems using a twin based method. Item level data can also be leveraged to boost statistical power in both twin and genomic studies.

Acknowledgements: I thank Sasha Gusev for his feedback.
Opinions/mistakes are my own.

1. Figure taken from Briley & Tucker-Drob 2015.